本文共 3130 字,大约阅读时间需要 10 分钟。
作为开发人员,每个人都有每个人擅长领域,自然也有自己不擅长的领域,很难成为完美的一个全栈开发。在面试中最怕遇见的一件事是面试官专挑你不擅长的领域进行提问,目的就是看你遇到问题的应变能力。

接下给大家分享一个面试中容易被问道知识点:“说说你对 binder 驱动的了解”,这个问题虽有些 “面试造火箭” 的无奈,可难点也是亮点、体现价值所在,是筛选面试者有效手段。如果让你回答,你能说出多少呢?我们来分别来看看A、B、C三位同学的回答如何吧!

A同学 :自认为无所不知,水平已达应用开发天花板,目前月薪 10k
面试官️:说说你对 binder 驱动的了解
A:binder 驱动是很底层的东西,在系统内核中,是 binder 机制的基石。
面试官:没了吗?把你了解的都说一下
A:直接让我说了解不好回答啊,还是问我问题吧
面试官:好,你刚才提到了系统内核,那介绍一下用户空间和内核空间吧
A:不知道,这东西了解了也没什么用啊!我对业务开发 API 比较了解,比如 RecycleView 布局,我写的贼溜~
面试官:好的,回去等通知吧

B 同学: 业余时间经常打游戏、追剧、熬夜,目前月薪 15k
面试官:说说你对 binder 驱动的了解
B:binder 机制分为四部分,binder 驱动、Service Manager、客户端、服务端。类比网络通信,Service Manager 是 DNS,binder 驱动就是路由器,它运行在内核空间,不同进程间通过 binder 驱动才能通信。
面试官:为什么 binder 驱动要运行在内核空间?可以移到用户空间吗?
B:不行,两个进程的进程空间有不同的虚拟地址映射规则,内存是不共享的,无法直接通信。Linux 把进程空间划分为用户空间和内核空间,分别运行用户程序和系统内核。
用户空间和内核空间虽也是隔离的,但可以通过 copy_from_user 将数据从用户空间拷贝到内核空间,通过 copy_to_user 将数据从内核空间拷贝到用户空间。
所以 binder 驱动要处于内核空间,才能实现两个进程间的通信。一般的 IPC 方式需要分别调用这两个函数,数据就拷贝了两次,而 binder 将内核空间与目标用户空间进行了 mmap,只需调 copy_from_user 拷贝一次即可。
面试官:从用户空间如何调用内核空间的 binder 驱动呢?
B:这个不了解了,我没看过 binder 源码,只是知道大概的通信方式
面试官:那你对 binder 驱动还有哪些了解,都说说吧
B:嗯… 没有了
面试官:好的,回去等通知吧

C 同学: 坚持每天学习、不断的提升自己,目前月薪 30k
面试官:说说你对 binder 驱动的了解
C:简单画张图吧:

面试官:你提到了驱动设备,那先说说 Linux 的驱动设备吧
C:Linux 把所有的硬件访问都抽象为对文件的读写、设置,这一"抽象"的具体实现就是驱动程序。驱动程序充当硬件和软件之间的枢纽,提供了一套标准化的调用,并将这些调用映射为实际硬件设备相关的操作,对应用程序来说隐藏了设备工作的细节。
Linux 驱动设备分为三类,分别是字符设备、块设备和网络设备。字符设备就是能够像字节流文件一样被访问的设备。对字符设备进行读/写操作时,实际硬件的 I/O 操作一般也紧接着发生。字符设备驱动程序通常都会实现 open、close、read 和 write 系统调用,比如显示屏、键盘、串口、LCD、LED 等。
块设备指通过传输数据块(一般为 512 或 1k)来访问的设备,比如硬盘、SD卡、U盘、光盘等。网络设备是能够和其他主机交换数据的设备,比如网卡、蓝牙等设备。
字符设备中有一个比较特殊的 misc 杂项设备,设备号为 10,可以自动生成设备节点。Android 的 Ashmem、Binder 都属于 misc 杂项设备。
面试官:看过 binder 驱动的 open、mmap、ioctl 方法的具体实现吗?
C:它们分别对应于驱动源码 binder.c 中的 binder_open()、binder_mmap()、binder_ioctl() 方法,binder_open() 中主要是创建及初始化 binder_proc ,binder_proc 是用来存放 binder 相关数据的结构体,每个进程独有一份。
binder_mmap() 的主要工作是建立应用进程虚拟内存在内核中的一块映射,这样应用程序和内核就拥有了共享的内存空间,为后面的一次拷贝做准备。
binder 驱动并不提供常规的 read()、write() 等文件操作,全部通过 binder_ioctl() 实现,所以 binder_ioctl() 是 binder 驱动中工作量最大的一个,它承担了 binder 驱动的大部分业务。
面试官:仅 binder_ioctl() 一个方法是怎么实现大部分业务的?
C:binder 机制将业务细分为不同的命令,调用 binder_ioctl() 时传入具体的命令来区分业务,比如有读写数据的 BINDER_WRITE_READ 命令、 Service Manager 专用的注册为 DNS 的命令等等。
BINDER_WRITE_READ 命令最为关键,其细分了一些子命令,比如 BC_TRANSACTION、BC_REPLY 等。BC_TRANSACTION 就是上层最常用的 IPC 调用命令了,AIDL 接口的 transact 方法就是这个命令。
面试官:binder 驱动中要实现这些业务功能,必然要用一些数据结构来存放相关数据,比如你上面说 binder_open() 方法时提到的 binder_proc,你还知道其他的结构体吗?
C:知道一些,比如:
| 结构体 | 说明 |
|---|---|
| binder_proc | 描述使用 binder 的进程,当调用 binder_open 函数时会创建 |
| binder_thread | 描述使用 binder 的线程,当调用 binder_ioctl 函数时会创建 |
| binder_node | 描述 binder 实体节点,对应于一个 serve,即用户态的 BpBinder 对象 |
| binder_ref | 描述对 binder 实体节点的引用,关联到一个 binder_node |
| binder_buffer | 描述 binder 通信过程中存储数据的Buffer |
| binder_work | 描述一个 binder 任务 |
| binder_transaction | 描述一次 binder 任务相关的数据信息 |
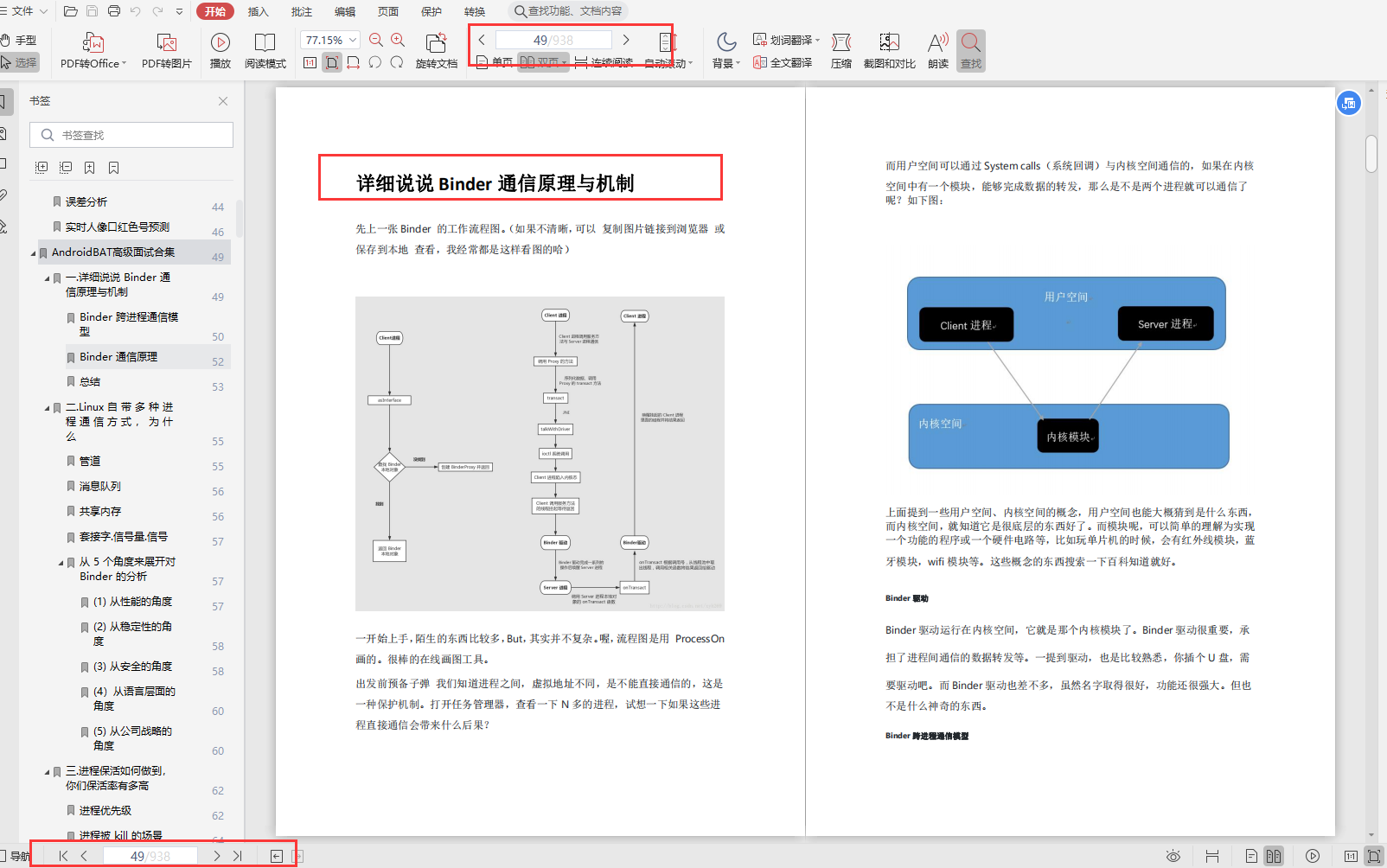
| binder_ref_death | 描述 binder_node 即 binder server 的死亡信息 |
其中主要结构体引用关系如下:

面试官:可以,我们再来聊聊别的。
如果你被问到了这些问题,你会怎么答呢?
针对面试中常见的问题,小编利用空闲的时间进行收集整理成了PDF学习文档,以备不时之需,望在以后的跳槽面试中能利用上。小编本想一一展现出来跟大家进行分享,但由于学习文档记录的内容知识点较多,暂且就用几张图展现一下吧!
如有想参考小编 PDF学习文档的可以直接去我 查阅,里面记录许多Android 相关学习知识点。
转载地址:http://exm.baihongyu.com/